对双标准数据压缩的一些认识-繁依Fanyi

Bicriteria data compression（双标准数据压缩）

文章目录

事接上回，当我继续想办法看懂 Brotli的第一阶段时，发现自己卡住了。毕竟自己的基础不是很好，只能想办法去解决，苦闷了一个下午，没办法，只能去死磕这一阶段参考的几篇论文。而我磕的四篇论文中的第一篇，就是这个—— 《Bicriteria Data Compression》。

一，关于 Abstract 部分

Abstract（摘要）部分主要围绕①需要解决的问题问题，②本文目标，以及③如何实现这个目标展开论述。

1. 问题：

这篇论文主要解决 LZ77解析的压缩空间大小和解压缩时间的问题。

2. 本文目标：

确定一个 LZ77 解析，在给定的时间T最小化压缩文件的空间占用
相应的，交换时间与空间两种角色，在预先给定压缩空间中最小化压缩时间

3. 如何实现目标：

引入新的 Bicriteria LZ77-Parsing 问题，它以一种原则性的方式形式化了数据压缩器传统上通过启发式方法处理问题
通过证明和部署加权图的一些特定结构属性，在 O(n log n²) 时间和 O(n) 空间字中有效地解决了这个问题，直到可以忽略的附加常数输入文件的 LZ77 解析
进行初步实验，表明我们所制作的新型压缩器对市面上高度工程化的竞争对手（如 Snappy，LZMA，Bzip2）都具有很强的竞争力。

二，关于 Introduction 部分

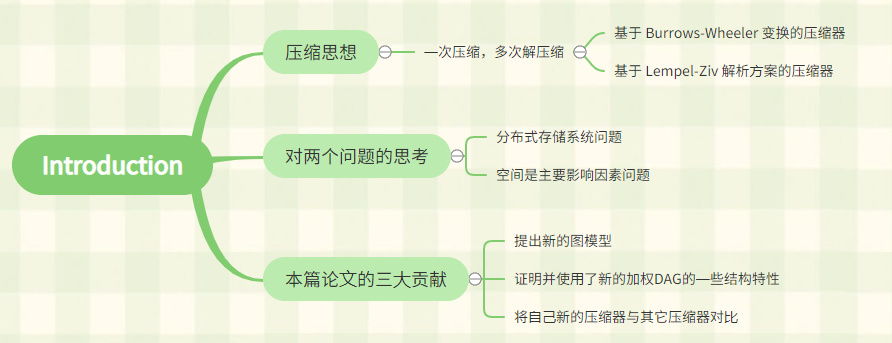
1. 压缩思想

随着海量数据集的出现以及随之而来的高性能分布式存储系统的设计,不少大厂纷纷行动，企图制作出一款可以实现有效压缩比和非常高效的解压缩速度的压缩器，例如 Google的BigTable ,Facebook的Cassandra,Apache的Hadoop等等，这些无不都重新点燃了科学界对更优秀的无损压缩器的设计的激情。

解决无损压缩器的有效压缩比与实现非常高效的解压缩速度之间的问题，打破性能瓶颈的方法有很多种，但从很多无损压缩器相关的论文中，都有一种思想：“compress once，decompress many times”。（参考多个翻译软件以及自己的理解，翻译为：一次压缩，多次解压缩）。

这种思想又可以被分为两大家族，①基于 Burrows-Wheeler 变换的压缩器和②基于 Lempel-Ziv 解析方案的压缩器。相信看过压缩算法入门论文的小伙伴《Universal lossless data compression algorithm》的这两种压缩算法一定不陌生，文中简要介绍了一下 Lempel-Ziv压缩算法，并详细说明了 Burrows-Wheeler变换。

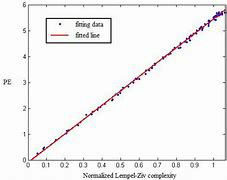
这两大家族的压缩器在压缩和解压数据时需要的时间都是线性的，并且需要的压缩空间可以用输入的K阶经验熵来约束。

2. 对两个问题的思考

一直以来，时间和空间似乎一直是算法中相互对立，但又相互依存的两个因素，经常刷 leetcode 的人一定对此深有感触，当我们解开一道算法题，很多人又会精进自己的算法，试图用“空间换时间”，“时间换空间”，以及尝试平衡两者来降低自己的执行用时和内存消耗，来获得更多的效益。

压缩算法也是如此，要么牺牲有效压缩比，要么牺牲解压缩速度，或者尝试用强大的技巧来平衡两者，一直以来研究这个无损压缩器的人归根到底都是在研究这个问题。然而只是研究这个似乎太困难了，于是这篇论文又尝试着从应用方面提出了两个具有挑战性的问题：

① 分布式存储系统问题（时间是主要影响因素）：

分布式存储系统，将数据分散存储在多台独立的设备上，可以拓展存储空间，Google，阿里等互联网公司，管理超过千万亿字节级别的大数据，它们对性能的要求很高，需要更低的解压缩时间。于是Snappy，LZ4等压缩器出现，帮助解决分布式存储系统上对解压缩时间要求更低的情况。

② 空间是主要影响因素的问题：

我们日常用的手机，手表，平板等等，这些设备对空间拓展比较难，需要尽可能在不改变其解压缩速度的情况下降低其压缩比，来让这些难以拓展内存的设备更好地利用内存。

3. Bicriteria Data Compression

Bicriteria Data Compression，本文也就是解决这个问题，下图是文中对其的描述。

简单描述一下，两个参数（输入文件S，限定时间T），解决一个目标（控制解压缩时间这个变量，尽可能的降低其压缩比），再反过来（控制其压缩比，尽可能地降低其解压缩时间）。

想要解决这个问题，我们就要解决两个因素：

① 将该双标准优化将在S的压缩版本中进行。

解决这个因素，文中采取基于LZ77的压缩器类别，因为它们在理论上和实践中占主导地位。使用主流的压缩器，可以借鉴前人经验，帮助我们解决更多的问题。

② 衡量待优化资源的计算模型

对于这个因素，可以从几个常用计算模型中得到启发，这些模型对多级内存层次和连续内存字的获取进行了抽象

4. 关于本篇论文的三大贡献：

1. 提出新的图模型

在《On the bit-complexity of Lempel-Ziv compression》中，提出了一个特殊的加权DAG，这个DAG由①n=|S| 个节点(nodes)，每个节点代表 S 的一个字符和②m=O(n²) 条边(edges)，每条边代表 LZ77 解析 S后可能出现的短语组成，就像下图。

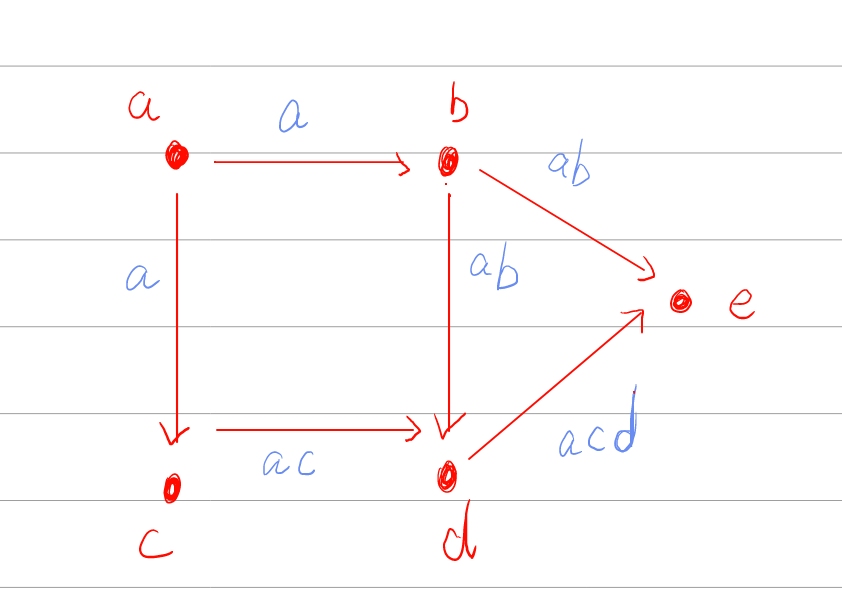
在本文提出了一个具有两个权重（时间权重，空间成本）的新的图模型，时间权重即解压缩短语的时间（根据上面提到的分层记忆模型派生），空间成本即用于计算存储与该边关联的 LZ77 短语所需的位数（根据压缩机中采用的整数编码器导出）

2. 证明并使用了加权DAG的一些结构特性

之后证明了上述的加权DAG的一些结构特性，使得我们能够设计一种算法，在 O(n log² n ) 时间和 O(n) 的工作空间内近似地解决我们版本的 WCSPP。

3. 将自己新的压缩器与其它压缩器对比

最后提出了一组初步的实验结果，将我们的压缩器的实现与最先进的基于LZ77 的算法（Snappy、LZMA、LZ4、gzip）和基于BWT的算法（具有有界和无界的内存占用）进行比较。

首先，它们为本文开始时提出的两个相关问题提供了实际依据，并为文中新颖的双标准数据压缩问题引入的理论分析。

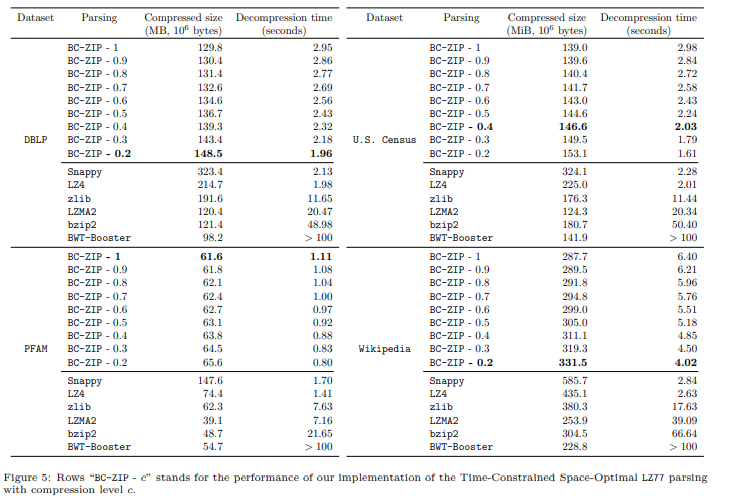
实验结果表现出文中解析策略通过表现出接近Snappy和LZ4（即已知最快的）的解压速度，以及接近基于BWT和LZMA的压缩器（即更简洁的）的压缩率，在所有高度工程化的竞争对手中占了优势。

参考

文章版权归作者所有，未经允许请勿转载。

THE END

未分类