关于 Burrows-Wheeler 变换和 Lempel-Ziv 解析的一些认识
文章目录
谈及数据压缩,简要概括其工作内容就是消除数据的冗余,其工作方式就是找到重复的模式,进行紧密的编码。
一,Burrows-Wheeler Transform
1. 概述
1994 年,Michael Burrows 和 David Wheeler 发明了Burrows-Wheeler Transform算法,并以他们的姓名命名。在读《Universal losslessdata compression algorithm》的时候,我也深刻体会到了文中对该算法精确的描述,以至于一半以上的内容都是讲它以及如何改进优化BWT的。

之前认为Burrows-Wheeler Transform 是一种压缩算法,但是后来看到一些博客,更加赞成BWT是一种数据转换算法,基于BWT可以发明出更多优秀的压缩器。被BWT转换后的数据更容易被压缩和搜索,举个经典例子:
通过BWT转换后,许多重复的字符将会被放在一起,此时进行压缩和搜索就会很容易。
2. 图解
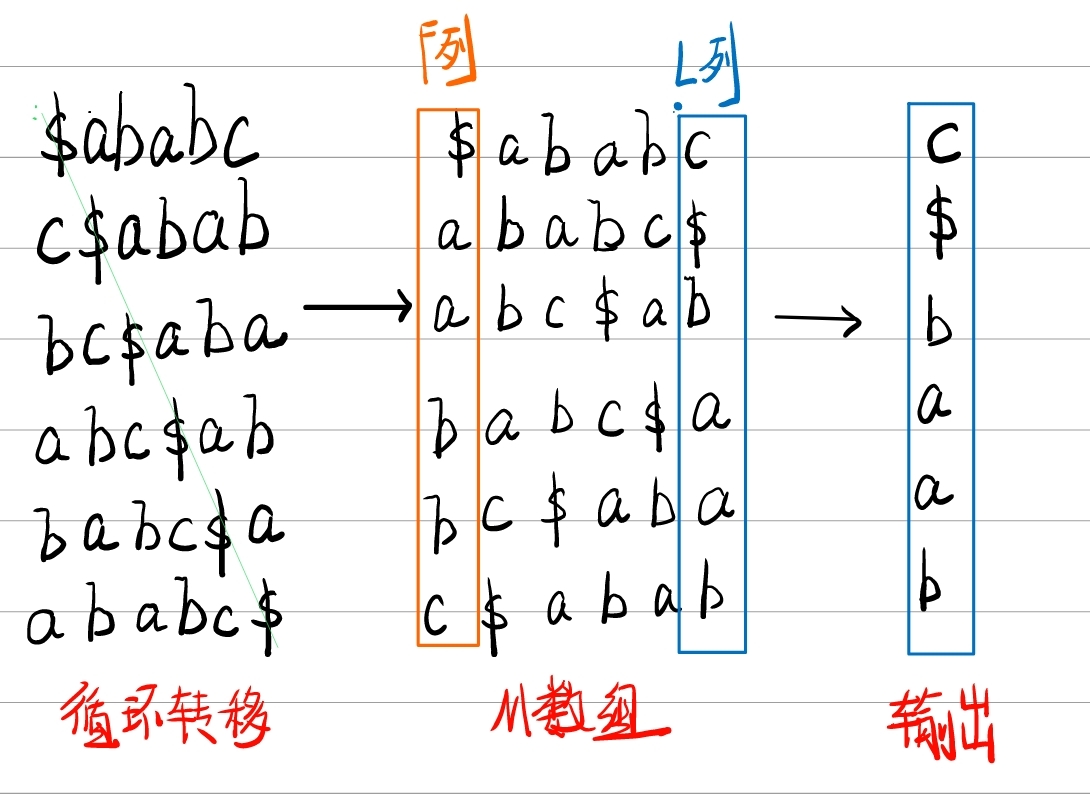
BWT就是一个加标记,循环转移,算出数组,输出结果的过程。
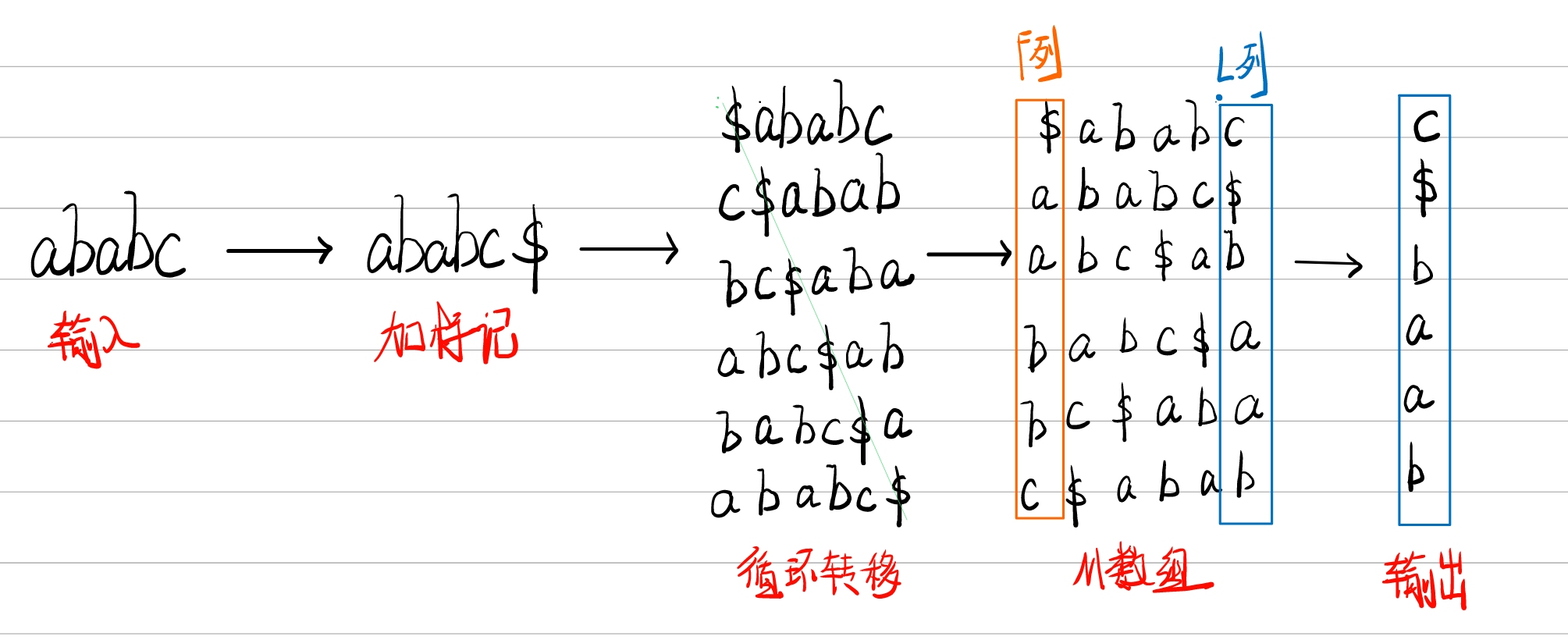
① 这里我们输入字符串ababc,并给其加上标记得到ababc$这个标记$要比所有字符都要小。
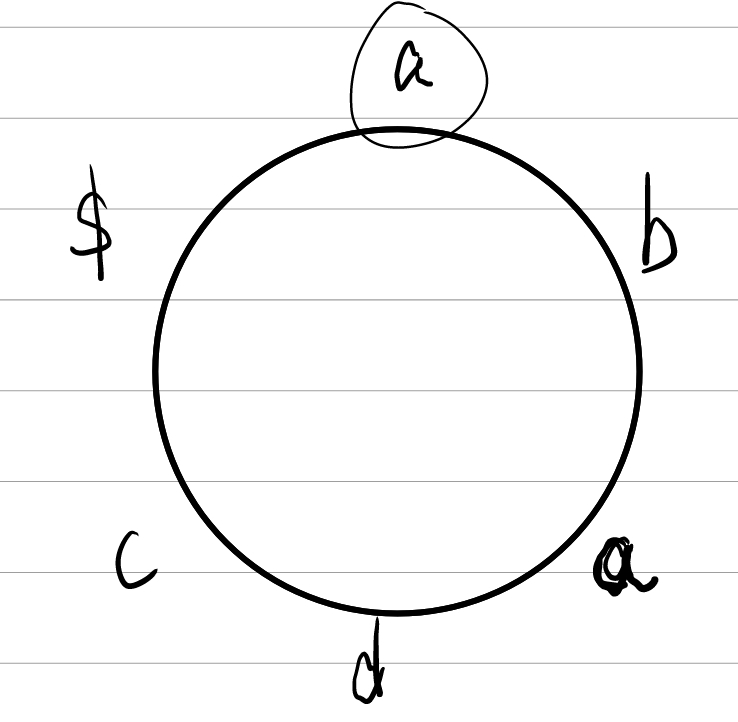
② 之后我们对处理后的字符串进行循环转移,此时你可以把ababc$当作一个圆,然后让其旋转,使得F列(第一列)的字符按照ASCII码从小到大排列。
③ 得到的M数组最后一列便是输出的L列
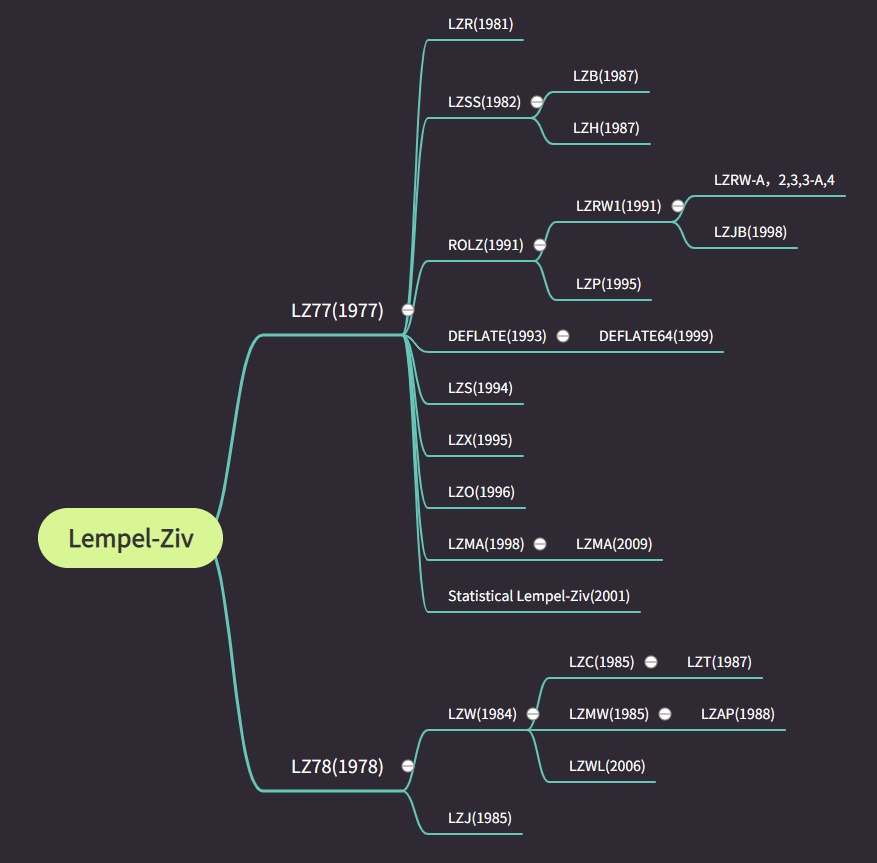
二,Lempel-Ziv Parsing
1. 概述
个人感觉,相较于上面一种算法,LZ系列算法可能更容易理解一些。
Lempel-Ziv 算法是由两位大佬 Abraham Lempel 和 Jacob Ziv 在论文《A Universal Algorithm for Sequential Data Compression》最早引入的。和 Burrows-Wheeler 算法一样,Lempel-Ziv也是由的名称也是由其发明者命名。
Lempel-Ziv 算法有两个版本,根据发明日期分别为 1977年的LZ77 和 1978年的LZ78,其后又衍生出了不少像deflate,lzx,lzma这样优秀的变体算法。
这里有一个比较有意思的事情,仔细看,你会发现先发明出的LZ77算法的变体比LZ78多,是因为LZ77被人们使用的时间长吗?并不是,这是因为LZ78算法在1984年被Sperry申请了其变体lzw算法的专利,并开始起诉相关软件供应商等在没有许可证的情况下使用率GIF格式,之后LZ78算法的普及逐渐衰减。尽管LZW的专利问题已经平息,并出现了很多 LZW变体,但目前只有在 GIF压缩中被普遍使用,占据主导地位的仍是LZ77算法。
尽管 Lempel-Ziv算法有很多变体,但它们都有一个共同的思想:如果一些文本不是均匀随机的,也就是说,所有字母出现的可能性不一样,那么已经出现过的子串会比没有看过的子串更可能再次出现。举个例子,在我们日常生活中,我们都有一些日用语,比如“你好”,“你好吗”;那么,“你好”,“你好吗”,“你好吗”中包含字串“你好”,我们便可以把“你好”简化为更短的二进制码,来替换“你好吗”中的“你好”,从而简化编码。
这样说可能还不清楚,举个LZ78编码的例子演示一下。
2. LZ78
LZ78 算法通过构建出现在⽂本中的⼦字符串字典来⼯作。
1. 图解
算法有两种情况:
- 若当前字符未出现在字典中,则将该字符编码进字典
- 若当前字符出现在字典中,则从当前字符开始与字符做最长匹配,并将匹配到的最长子串后的第一个字符做特殊处理,并编码进字典。
最直接的讲解算法的方式应该就是画图了
举个例子:假设我们有字符串 AABABBBABA ,我们使用 LZ78算法对其进行压缩
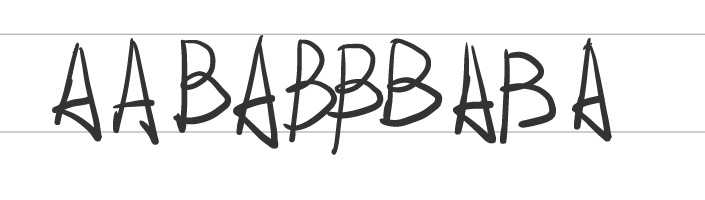
① 先从左边最短并从未出现过的短语开始,这里是A,放入字典。
② 接下来考虑剩下的字符串,由于之前已经见过A了,匹配最长字串A,并取最长字串的下一个字符做特殊处理,取AB放入字典
③ 再考虑剩下的字符串,由于之前已经见过A了,继续匹配下一位B,此时最长字串为AB,继续匹配下一位,未匹配到最长字串,取ABB编入词典
④ 考虑剩下的字符串,第一个字符是B,未匹配到最长字串,编入词典

⑤ 同理,匹配剩下的字符,匹配到最长字串AB,连同下一位编入词典
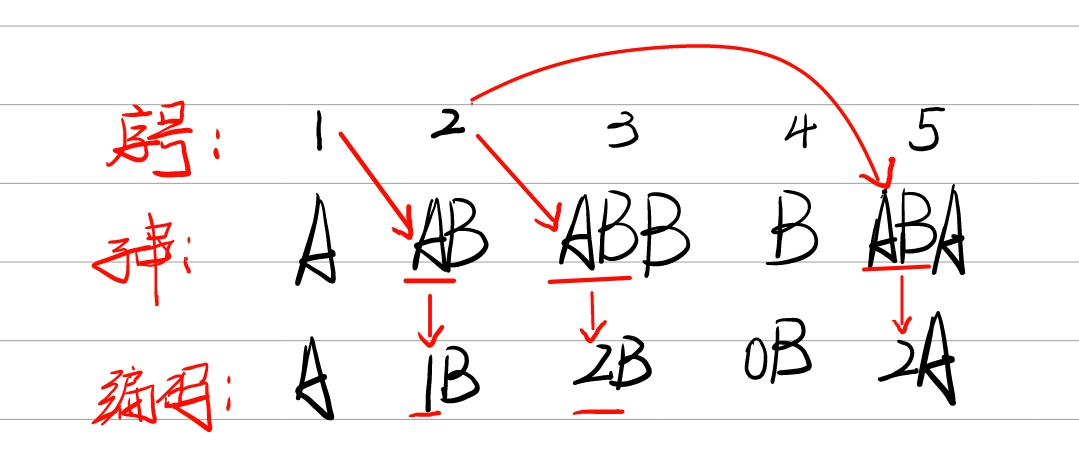
由于序号(index)2的字串AB中有A,可以用A的序号来替换字串A,编码AB为1B。同理,序号(index)3的字串ABB中有最长字串AB,可以用AB的序号替换ABB中的AB,编码为2B。序号(index)4的字串B与前面的字串没有匹配,为空集Ø,编码为0B。序号(index)5的ABA编码为2A。
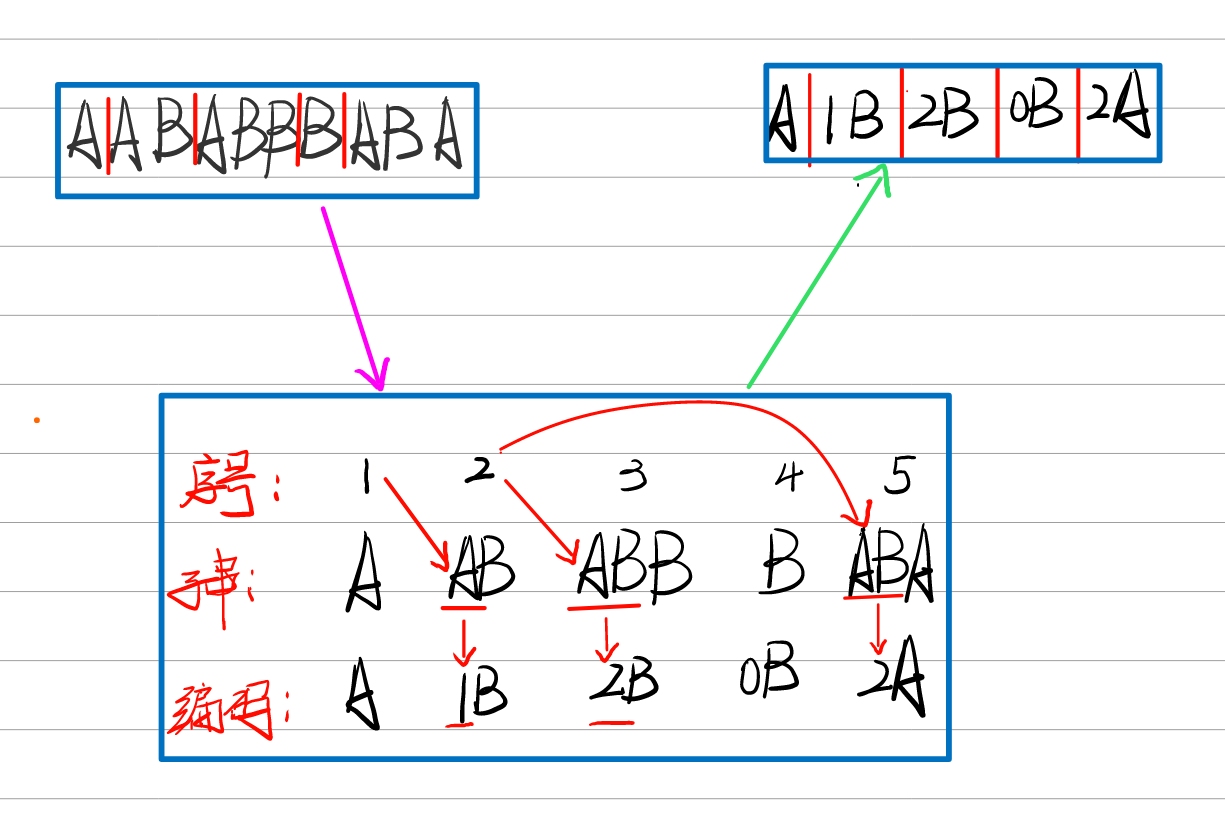
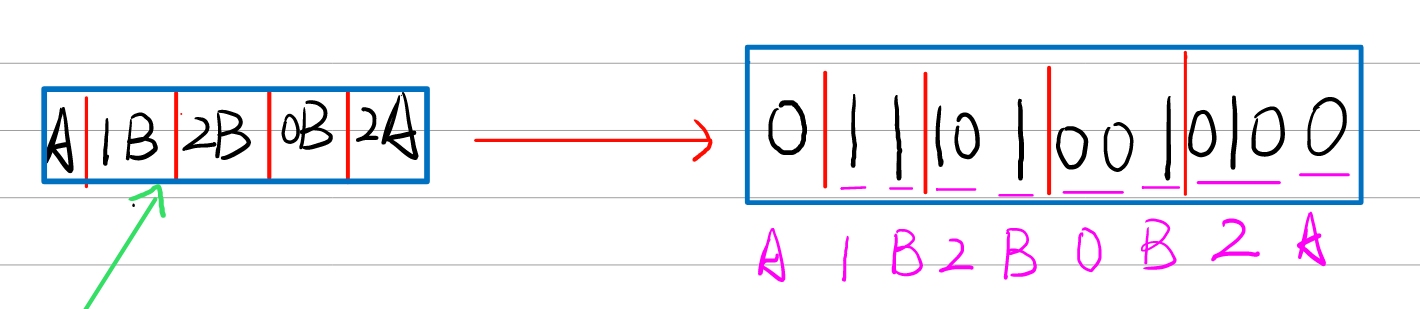
此时,我们就用字典将原来的字串编码成了一个更简单的串,简化了相关变量,此时我们只需要给A和B赋值即可得到最终编码的二进制串。这里假设A=0,B=1。
- LZ78 算法动态构建其字典,只遍历数据一次,这意味着不必在开始编码之前接收整个⽂档。
Overview – The Hitchhiker’s Guide to Compression (go-compression.github.io)




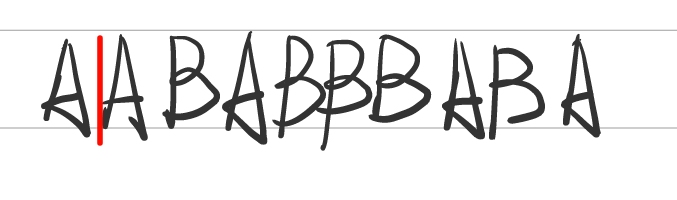







暂无评论内容